03/11/2020 posted
When a signal is amplified by a preamplifier, the noise generated inside the amplifier is applied to the output signal. In other words, when evaluating the performance of an amplifier, it is necessary to consider the noise generated inside the amplifier.
However, because of the amplifier's gain, it is very difficult to consider internal noise and gain at the same time. Therefore, we have assumed that the amplifier is ideal, which means it does not generate any internal noise. Meanwhile, the internal noise is converted to be noise generated from outside, where is known as the input terminal. And this is called the Equivalent Input Noise. In this way, the noise and gain of an amplifier can be considered independently.
Fig. 1 Model Diagram Equivalent Input Noise
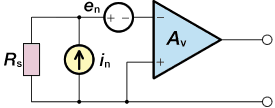
There are two types of amplifier noise: voltage noise (en) and current noise (in). From the model in Fig. 1 with the signal source impedance as Rs, the equivalent input noise voltage is defined by the following equation.
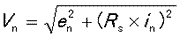
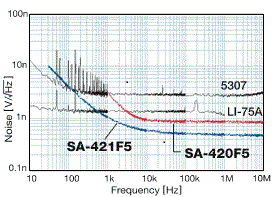
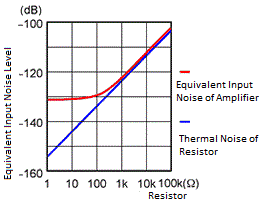
Amplifier noise generally increases as the frequency decreases, as shown in Fig. 2. Also, it cannot be any lower than the noise generated by a resistor with the same amount of resistance as the signal source impedance (see Fig. 3).
Fig.2 Example of Noise Frequency Response
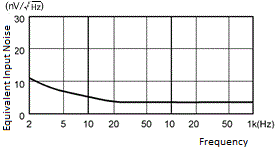
Fig.3 Amplifier and Resistor Noise Levels
Similarly, sensors and resistors inside circuits can also generate noise. The noise of resistor is called Johnson-Nyquist noise (thermal noise), which is proportional to the temperature. Therefore, the noise level at room temperature is most commonly calculated. These noise levels are often expressed in terms of voltage density (nV / √Hz) per unit of bandwidth(1Hz) .
The equivalent input noise is the result of output noise divided by the gain. When comparing the noise levels between two or more amplifiers, we cannot just simply compare their equivalent input noises due to difference in frequency responses between amplifiers.
In order to compare amplifiers, there is a way of measurement where we can analyze the output noise first then determine the voltage density of the equivalent input noises. The output noise voltage density divided by the gain of the amplifier is called the equivalent input noise voltage density. Equivalent input noise voltage density can be compared regardless of the frequency bandwidth of the amplifier. However, due to the frequency response of the density, frequency conditions must be considered (Fig.4). Assuming that the frequency response of the noise voltage density is flat, then 35 µV / √500 kHz = 49.5nV / √Hz.
Fig.4 Comparison of Noise Levels among preamplifiers