離散フーリエ変換(DFT)
- Discrete Fourier Transform
- 离散傅里叶变换
- 이산 푸리에 변환
フーリエ変換は、時間領域関数(波形)を周波数領域関数(スペクトラム)に変換する演算である。連続関数を対象としており、A/D変換器でサンプリングして得られるような離散的な値(波形データ)に対しては、DFT(離散フーリエ変換)で時間領域→周波数領域への変換を行う。ディジタルデータに対する演算なので、“ディジタルフーリエ変換”とも呼ばれる。画像/音声圧縮等広く利用されているが、ここでは計測用途でのDFTについて説明する。
FRA(周波数特性分析器)やLCRメータでは、内蔵発振器より正弦波を出力して試料に与え、大きさ/位相が変化した信号をA/D変換でサンプリングして、ディジタルデータに変換し、DFT演算により測定周波数成分の大きさ(振幅)と位相を求める。測定周波数成分だけが必要なので、基本波成分だけの1次のフーリエ係数を求める演算を行っている。下図はFRA(周波数特性分析器)の分析部のブロック図である。点線内での、位相検波~平均化部分がDFT演算である。ω=2πf で、fは測定周波数である。
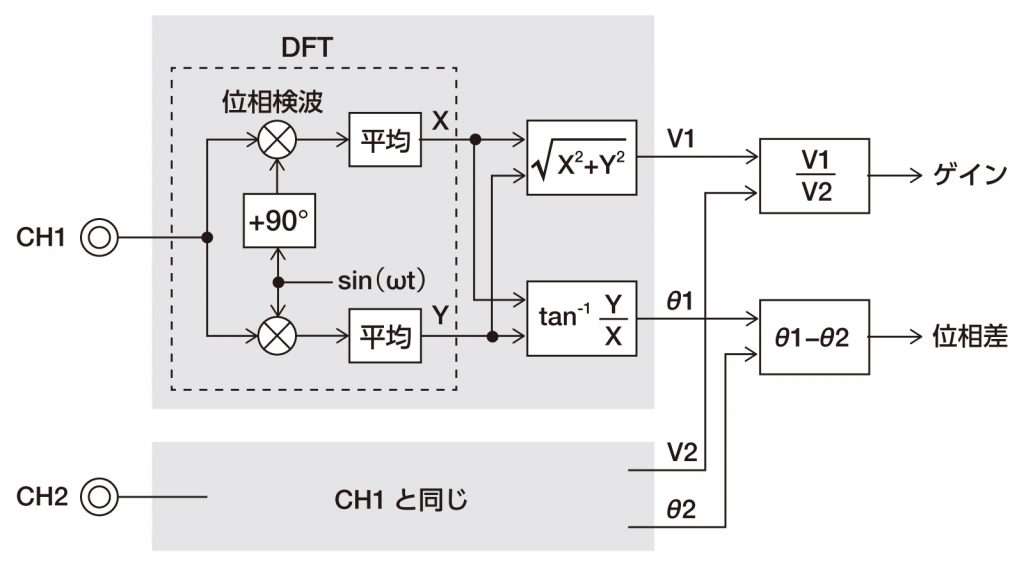
DFTで得られた値(上図でのX , Y)は、各々入力信号の測定周波数成分における実部、虚部に相当する。その後必要に応じて、絶対値(V1 , V2)や位相(θ1 , θ2)を計算で求めて、チャネル間のゲインと位相差を計算する。これはFRAでの演算で、LCRメータの場合にはCH1に電圧信号、CH2に電流信号を入力することにより、ゲインはインピーダンス絶対値|Z| に相当する結果になる。
(連続関数の)フーリエ変換は、[無限の過去]~[無限の未来]の、無限に長い時間の波形を必要とする。一方、現実の計測で用いられるDFT演算は、有限の時間の波形を用いて計算するが、以下のように計算に使用する(切り出した)波形が無限に繰り返しているものとして計算が行われる。したがって、分析範囲を整数周期としないと、波形の始まりと終わりがきれいに繋がらなくなり、リーケージ誤差と呼ばれる誤差が生じる。
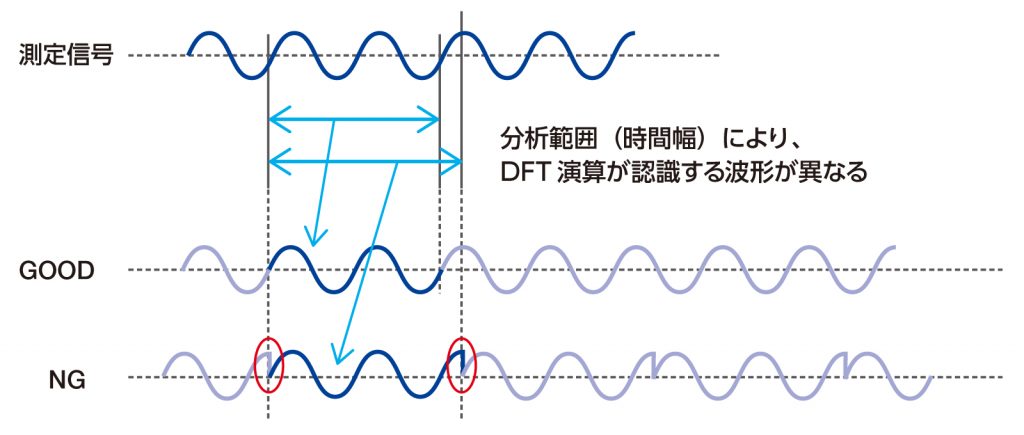
FRAやLCRメータでは、A/D変換器のサンプリングクロックや取り込みワード数等を調整して、DFT演算に使用する波形が整数周期となるように高精度に制御しているので、リーケージ誤差が生じることはない。しかし、FFTアナライザでは未知の周波数成分を扱うので、リーケージ誤差が生じる。窓関数の使用で改善できるが、完全ではないので、注意が必要である。
FFTアナライザで使用されているFFT(Fast Fourier Transform、高速フーリエ変換)アルゴリズムも、ディジタルデータに対する変換という意味でDFTの一種である。DC、基本波、高調波の各フーリエ級数を一度に効率良く、高速に計算できることが特長であるが、周波数分解能に制約がある。特に、高い周波数で周波数分解能を高く保つことが困難である。