プリアンプとフィルタの使い方
プリアンプとフィルタの使い方
プリアンプとフィルタの使い方
最適なプリアンプとフィルタの選び方
音、光、振動、圧力、温度などあらゆる現象は、センサで電気信号に変換されることにより、計測・分析・制御が可能となります。
現象が微少であれば、センサから得られる電気信号は小さくなるため、信号を増幅する必要があります。
小さな信号はノイズの影響を受けやすく、たとえばセンサ自身の発生するもの、センサやその電源や出力ケーブルに飛び込むもの、アンプが発生するもの、アンプの出力側に飛び込むものなどなど、計測はさまざまなノイズとの戦いといっても過言ではありません。
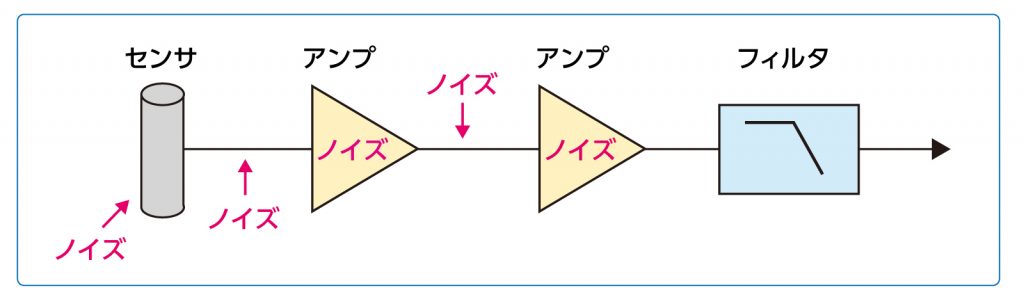
そこで・・・
- センサとアンプ間ではケーブルをできるだけ短くする
- シールドを施す
- 差動入力を検討する
など、ノイズを受けつけにくい方法を採用します。
また、
- ノイズの発生をできるだけ抑えたアンプを使用し、
さらに、
- フィルタを用いて必要以外の周波数帯域の信号やノイズをカットする
ことが必要となります。
この特集では、これらのノイズ対策のうち、自らの発生するノイズが少ないプリアンプと、不要な信号を適切に除去するフィルタをご紹介します。
正しい計測に不可欠なプリアンプやフィルタですが、計測の前処理に使用するものなのに、設計や調整が面倒なため、余分な手間がかかってしまう・・・ということがありませんか?
ここで取り上げるプリアンプとフィルタは、電源とわずかな部品を準備するだけで、特に電気の専門でない方でも簡単に使用できるものです。 手間をかけない高精度な信号前処理を、実現できます。
ここからは、プリアンプとフィルタを分けて説明します。
プリアンプ
理想のアンプとは?
アンプの最大の使命は、入力信号を忠実に増幅できることです。
理想のアンプとは、
- 十分な周波数帯域を持っている。
- アンプ自身がノイズを発生しない。
- 波形ひずみがない。
- 温度や経時変化に対して安定。
しかし、実際にはいろいろな条件の中で、もっとも満足のいくアンプを採用することになります。
アンプのノイズ
アンプは、「自分自身がノイズを発生しない」というのが理想です。しかしながら、必ずアンプはノイズを発生します。アンプのノイズがどれくらい影響するものなのか?
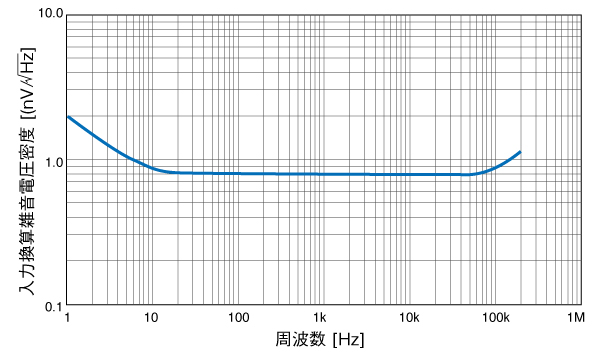
アンプ内の各所で発生するノイズが、すべてアンプの入力箇所で発生したものと仮定したノイズを「入力換算雑音」で表します。
アンプの入力換算雑音レベルが信号入力レベル以上であれば、信号はアンプ自身の発生するノイズに埋もれてしまいます。
微少信号を増幅する場合は、特に入力換算雑音レベルと信号入力レベルの比が重要になります。
アンプの雑音は・・・・
- 低い周波数では1/fのノイズがあり、周波数が低い程大きくなります。
- 高い周波数でもノイズが増加します。
- ノイズの分布が平坦な周波数帯域では、ノイズレベルは周波数帯域の平方根 (√) に比例します。
- 信号側(信号源) のインピーダンスによっても影響を受けます。
アンプの入力側のSN比と出力側のSN比を比較したものが、「ノイズフィギュア」です。
信号源インピーダンスと信号周波数とノイズフィギュアの関係を等高線のように表した特性図がよく用いられます。
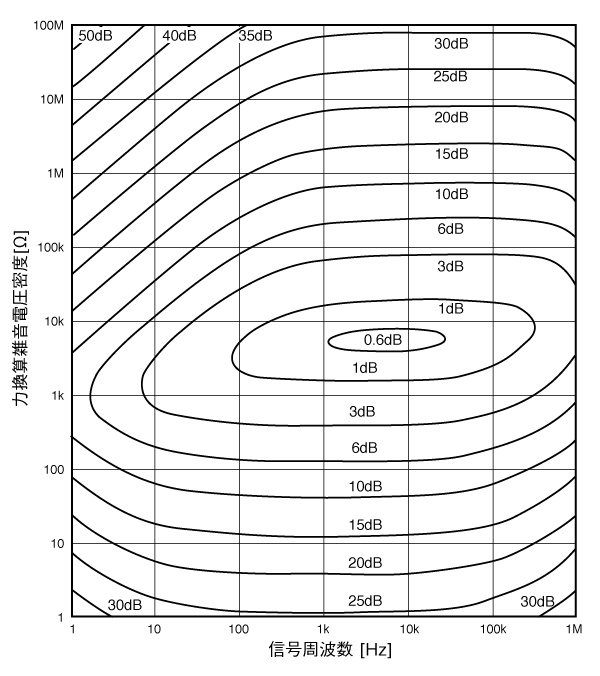
ノイズの実例とアンプの組み合わせ例
プログラマブルゲインアンプ CA-206L2の場合
CA-206L2は、
入力換算雑音:1kHzで7nV/√Hz(typ.)
G=最大100
周波数帯域:500kHz
ですから、
7×√(500×1000) =4,949nV
約5μVです。
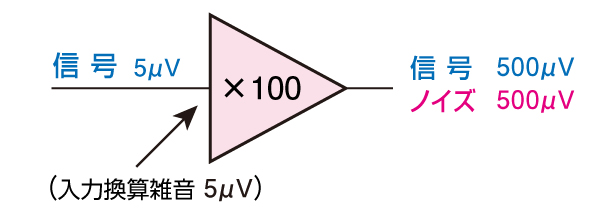
利得が100倍の時、出力では500μVなので、5μV以下の入力信号は、ノイズに隠れてしまいます。
信号が5μV、ノイズも入力側に5μV存在することと等価のため、出力ではノイズと信号が同レベルになってしまいます。
低雑音増幅器 CA-261F2の場合
CA-261F2は、
入力換算雑音:1kHzで0.8nV/√Hz(typ.)
G=100
周波数帯域:200kHz
ですから、
0.8×√(200×1000) =358nV です。
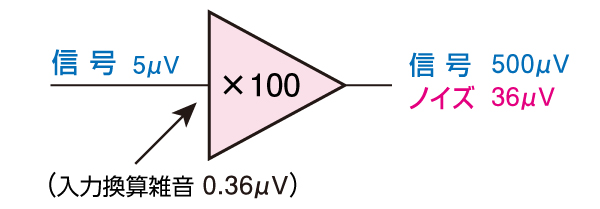
利得100倍で出力は約36μVとなり、CA-206L2の1/10以下です。
アンプが発生するノイズが小さいので、十分なS/Nが得られます。
それでは、上のCA-261F2とCA-206L2を組み合わせて、10万倍 (100dB) 増幅してみます。
(入力信号 5μV)
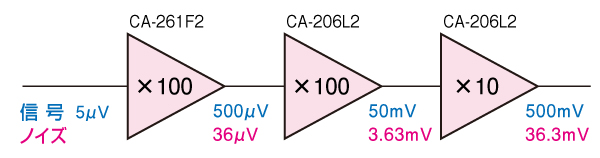
図の2段目のアンプの出力ノイズは・・

この例のように、アンプを組み合わせて増幅するときは、アンプ自身のノイズを考慮して、初段には低雑音アンプ使用することが、ポイントとなります。
プリアンプを選択するポイント
増幅したい信号のレベル
信号のレベルが極端に小さいため、アンプを数段使用して、利得を設定する場合があります。この時、初段のアンプで発生したノイズは、後段で増幅されるため、初段には特に低雑音タイプのアンプを使用します。
信号の周波数範囲
周波数の下限は直流から必要か? 上限の周波数は?
帯域の広いアンプは高速応答し、波形の立ち上がりが忠実です。しかし、帯域が広いアンプというのは、ノイズも多くなりますので、必ずしも帯域が広ければいいというものではありません。
利得の切換え
利得は、固定タイプと切換えタイプがあります。利得を変化させる用途には、切換えタイプを選択します。
入力・出力のインピーダンス
低周波のアンプの理想は、十分に高い入力インピーダンス、低い出力インピーダンスです。
入力モード
通常は片線接地ですが、接続される入力信号がグラウンドから電位 (同相ノイズ) を有している場合には、差動入力が有効です。差動入力タイプのアンプを使うと、その電位がキャンセルされます。
差動入力のアンプを選択する際は、同相入力の信号除去能力 (CMRR) が十分大きく、安定していることがポイントとなります。
その他
最大出力電圧、出力ノイズ、出力オフセット、オフセットドリフト、ひずみ、形状、電源、消費電力なども考慮する必要があります。
センサの出力が電流出力の場合は、電流/電圧変換増幅器 (I/Vアンプ) を選択
選択のポイント
- 低入力インピーダンス
- 信号源の容量が総合周波数特性に影響大 → センサとアンプの入力ケーブルを最短に設定
エヌエフのプリアンプ
エヌエフは、低雑音プリアンプを豊富に取り揃えています。
「プリアンプを選択するポイント」をチェックしながら、最適な製品をお選びください。
CAシリーズ
| 型名 | 品名 | 入力形式 | 入力抵抗 | 入力換算雑音 | 周波数特性 | 利得 | 入出力 位相 |
出力抵抗 | 特長 |
|---|---|---|---|---|---|---|---|---|---|
| CA-261F2 | 低雑音増幅器 | 不平衡 片線接地 |
100kΩ | 0.8nV/√Hz | DC~200kHz | 100倍 | 同相 | 50Ω | 低雑音 |
| CA-271F4 | 低雑音FET増幅器 | 不平衡 片線接地 |
1MΩ* 1GΩ以上 |
1.6nV/√Hz | DC~10MHz | 100倍 | 同相 | 50Ω | 低雑音 広帯域 |
| CA-271F5 | 低雑音FET増幅器 | 不平衡 片線接地 |
1MΩ* 1GΩ以上 |
1.6nV/√Hz | DC~20MHz | 100倍 | 同相 | 50Ω | 低雑音 広帯域 |
| CA-461F2 | 低雑音差動増幅器 | 差動 | 100kΩ | 1.5nV/√Hz | DC~200kHz | 100倍 | 同相 | 50Ω | 低雑音 差動入力 |
| CA-406L2 | 差動増幅器 | 差動 | 30GΩ | 27nV/√Hz | DC~200kHz | 1, 2, 5, 10, 20, 50, 100倍 | 同相 | 50Ω | 差動入力 利得切換え |
| CA-206L2 | プログラマブル ゲインアンプ |
不平衡 片線接地 |
1MΩ | 7nV/√Hz | DC~500kHz | 1, 2, 5, 10, 20, 50, 100倍 | 同相 | 50Ω | 利得切換え |
| CA-102R3 | 高速インバーティングアンプ | 不平衡 片線接地 |
入力抵抗による | DC~10MHz 利得による |
1~10 | 反転 | 5Ω | 広帯域 | |
*1-2番ピン短絡時
電流入力アンプ
| IV-204-F3 | 電流/電圧変換増幅器 | 不平衡 片線接地 |
1kΩ | 70fA/√Hz | DC~1MHz | 4×106 (V/A) | 同相 | 50Ω | 低雑音、広帯域 |
|---|---|---|---|---|---|---|---|---|---|
| IV-202-F4 | 電流/電圧変換増幅器 | 不平衡 片線接地 |
25Ω | 450fA/√Hz | DC~10MHz | 1×105 (V/A) | 同相 | 50Ω | 低雑音、広帯域 |
さらに低雑音なアンプは・・・
プリアンプの利得設定
ここでは、当社のプリアンプの中で、利得の切換えができるプログラマブルフィルタ CA-206L2、差動増幅器 CA-406L2 (エヌエフの低雑音なプリアンプ参照)を例に、利得の設定方法をご紹介します。
プログラマブルゲインアンプCA-206L2、差動増幅器CA-406L2の利得設定
CA-206L2/CA-406L2は、1, 2, 5, 10, ×1, ×10の計6本のコントロール端子を、TTLまたはCMOS負論理で制御して、利得を設定します。


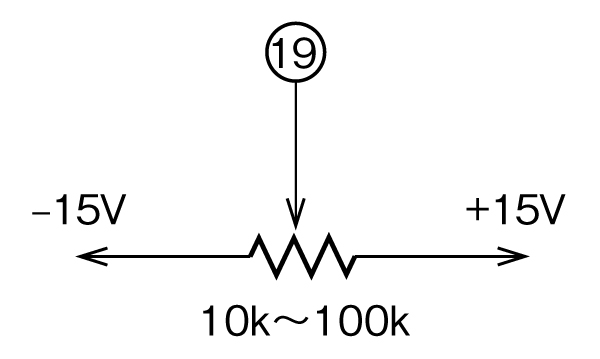
固定またはスイッチによる設定
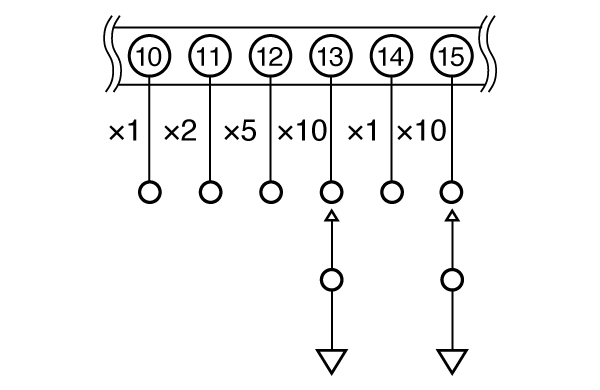
(10)~(13)は×1~×10を、(14), (15)は×1, ×10を設定します。
左の図は、10×10=100倍の設定となります。
(10)~(13)のいずれか1点および(14), (15)のいずれかが常に0Vになるようにする。
バイナリラッチアダプタ CA-903Nを使った設定
CA-206L2/CA-406L2は、バイナリラッチアダプタ CA-903N を組み合わせることにより、利得をバイナリコードで行え、さらにラッチ機能を持たせることができます。
ラッチ制御入力端子を開放または+5Vにすると、利得設定バイナリコード入力がスルーとなり、負論理のレベル信号で利得設定が可能となります。
ラッチ機能を働かせる時は、ラッチ制御入力を0Vにします。0Vになるエッジで、利得設定バイナリコード入力の情報がラッチされます。

CA-206L2とCA-903Nの組み合わせ
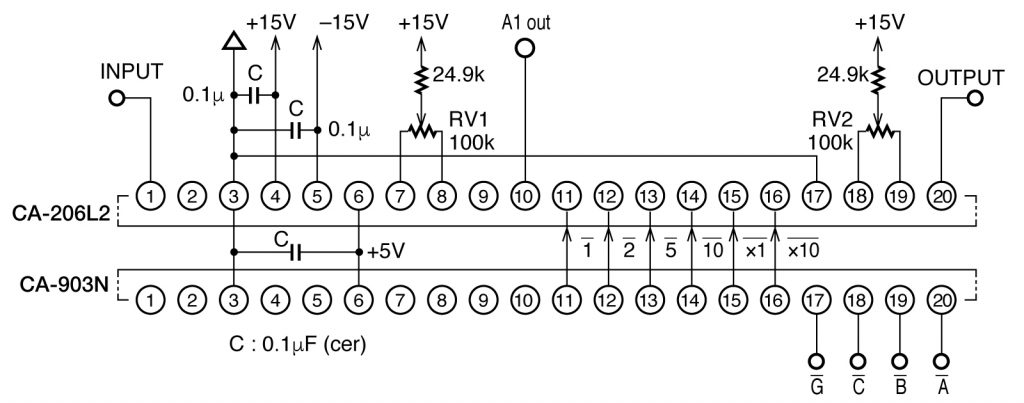
CA-406L2とCA-903Nの組み合わせ
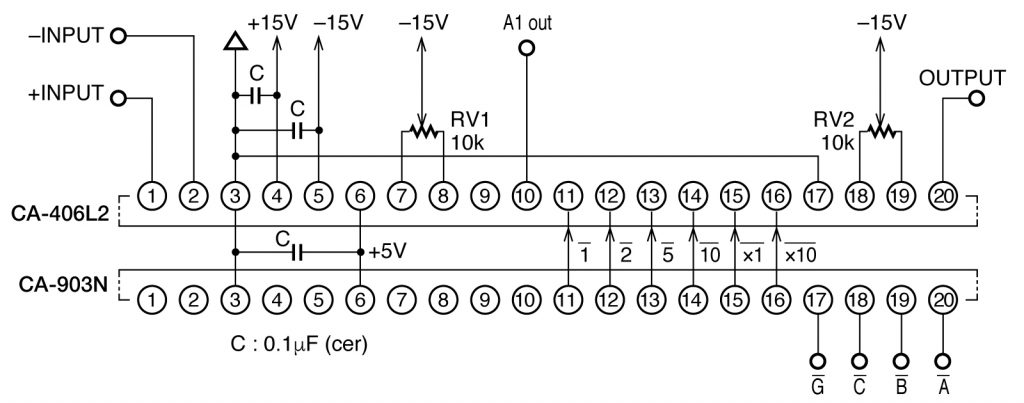
フィルタ
フィルタの種類と理想特性
ご存じの通り、エレクトロニクスの世界のフィルタとは、 色々な周波数成分を持つ信号の中から、不要な周波数成分を除去し、必要な周波数成分のみを取り出す回路のことです。
プリアンプ同様、計測の前処理で使われるワキ役ですが、設計や調整は結構面倒で、フィルタを自作するのは、かなり大変なことです。
ここでは、プリアンプ同様、モジュールを使って、設計や調整の手間を省いて、フィルタを使うポイントをご紹介していきます。
はじめにフィルタの種類やフィルタで使われる用語などをまとめておきます。
理想のフィルタとは?
必要な信号をきれいに取り出すためには ・・・
- 信号の大きさが変化しない →通過域の利得がフラット
- 波形が変化しない →ひずみがゼロ
- 余計な信号を付加しない →ノイズがない
不要な信号をきれいに取り除くためには ・・・
- 不要な周波数帯では利得がゼロ →減衰域の利得がゼロ
さらに・・・
通過域と減衰域は、遮断周波数の点で (遷移域なしで) 切り換わる。
以下の図は、ローパス、ハイパス、バンドパス、バンドエリミネーションの4種類のフィルタの理想特性を表したものです。
ローパスフィルタ (LPF)
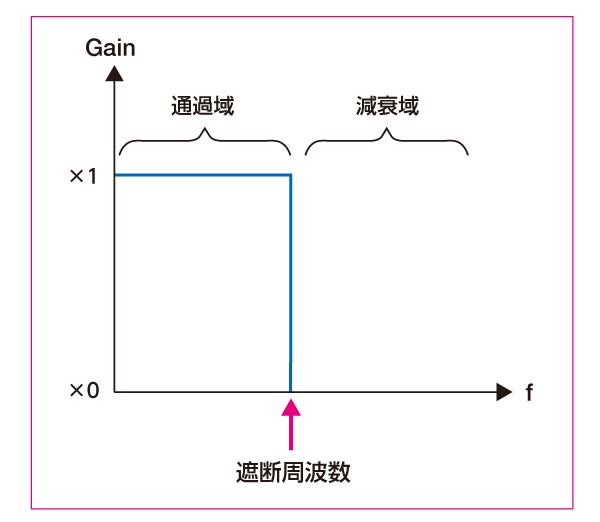
▼
遮断周波数より低い信号を通す。
ハイパスフィルタ (HPF)
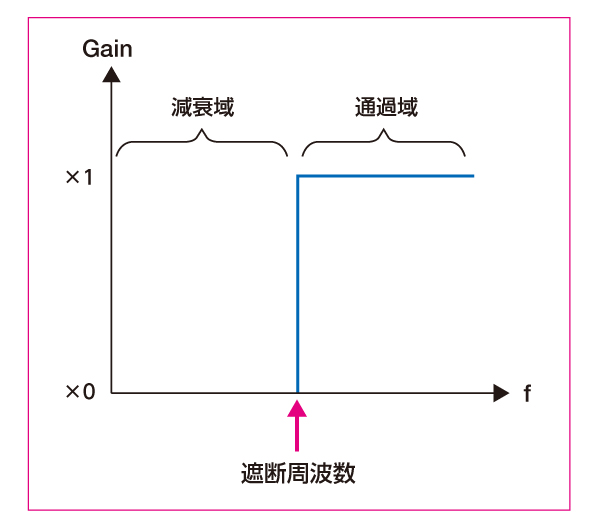
▼
遮断周波数より高い信号を通す。
バンドパスフィルタ (BPF)
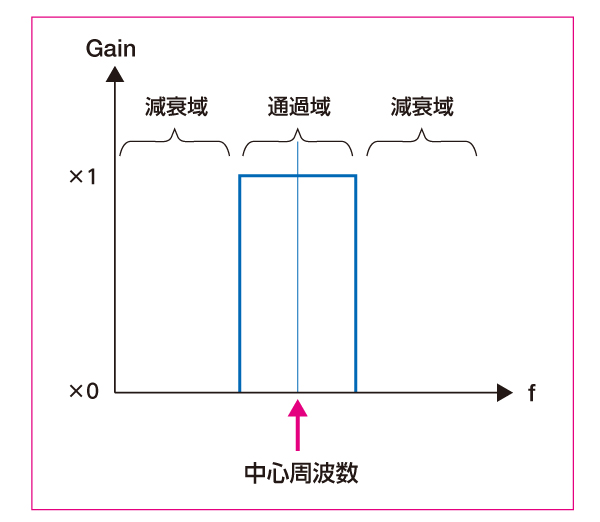
▼
必要な周波数帯域の信号を通す。
バンドエリミネーションフィルタ (BEF)
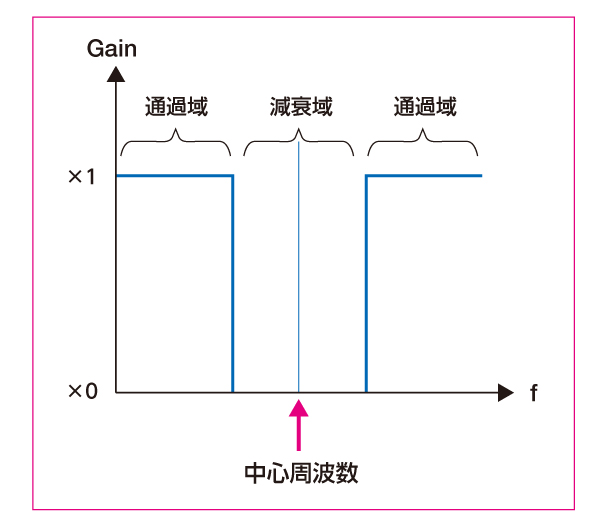
▼
中心周波数近辺の信号だけ取り除く。
フィルタで使われるおもな用語
通過域
フィルタで取り出したい信号の周波数帯域減衰域
減衰域
フィルタで除去したい信号周波数帯域
遮断周波数
遮断周波数通過域と遮断域の境界の周波数
中心周波数
バンドパスフィルタ、バンドエリミネーションフィルタの通過域、減衰域の中心の周波数
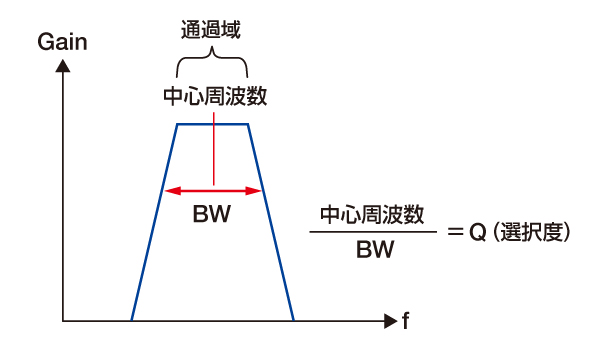
選択度 (Q)
バンドパスフィルタ、バンドエリミネーションフィルタで通過域、減衰域の幅 (BW) を示すパラメタ
Q=中心周波数/BW
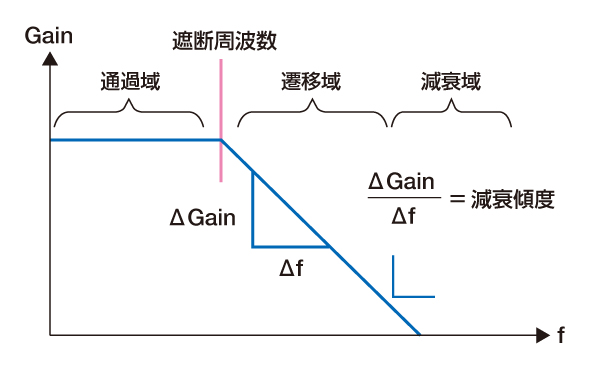
遷移域
通過域と減衰域の間の周波数特性が、通過域から減衰域へと変化してゆく途中の状態の周波数域
減衰度
減衰域での減衰度合
減衰傾度
遷移域でのフィルタ特性の傾き。
一般的にdB/oct、dB/decという単位で示される
dB/oct:オクターブ(2倍)周波数が変化したときにどれだけ減衰するか
dB/dec:ディケード(10倍)周波数が変化したときにどれだけ減衰するか
次数
次数理想特性を近似する関数の次数
次数が高いほど理想に近い
フィルタの特性と特徴
理想のフィルタにできるだけ近いフィルタを実現するためのアプローチとして、いくつかの方法が確立していて、それらがフィルタ特性のバリエーションとなっています。
通過域特性や減衰傾度など、重視する特性が最適になるようなフィルタ特性を選択します。
ここでは、フィルタ特性のバリエーションとそれぞれの特徴をご紹介していきます。
- 通過域をフラットにすることを重視:バターワース
- 立ち上がり特性を最適にする:ベッセル
- 通過域を犠牲にして遮断周波数近辺での減衰傾度を重視:チェビシェフ
- 通過域、減衰域ともに犠牲にして遷移域をできるだけ狭くする(減衰傾度が大きい):連立チェビシェフ(楕円、エリプティック)
4次ローパスフィルタの例
バターワース
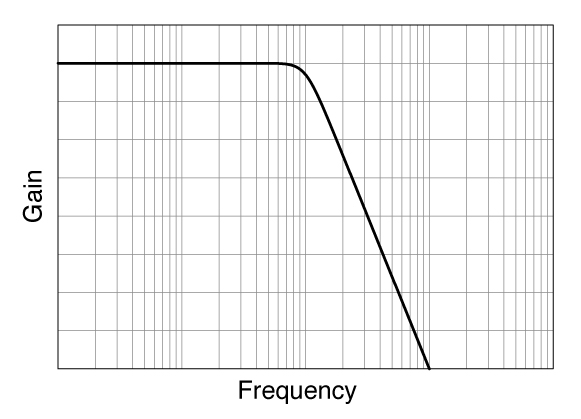
- 構成しやすく一般的
- 通過域がフラット(最大平坦特性とも呼ばれる)
- 減衰傾度が、次数×6dB/oct
【用途】
- 通過域にフラットネスが必要な場合
- 設計や構成を簡単にしたい
- 分離したい信号の周波数帯が比較的離れている場合(10倍程度)
ベッセル
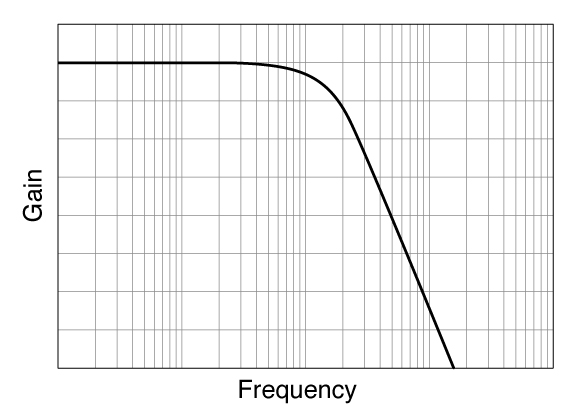
- 過渡応答 (立ち上がり/立ち下がり) 特性を最適化(LPFのみで有効)
- リンギング、オーバシュートが最小かつ立ち上がりが同一の次数のフィルタ中で最速
【用途】
- 波形に情報がある場合
- 過渡応答をきれいに整えたい場合
チェビシェフ
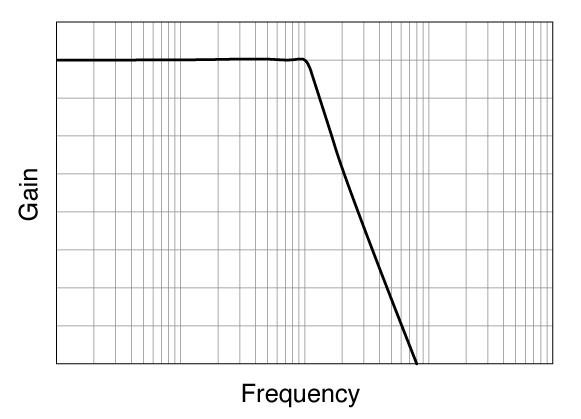
- 通過域にリプル (うねり) を持たせることで、遮断周波数近辺の減衰傾度を大きくした特性
- 回路構成はバタワースと同程度であるが、設計に手間がかかる
- 過渡応答でリンギングが大きい
【用途】
- バタワース程度の回路構成で、減衰傾度を少し大きくとりたい場合
連立チェビシェフ
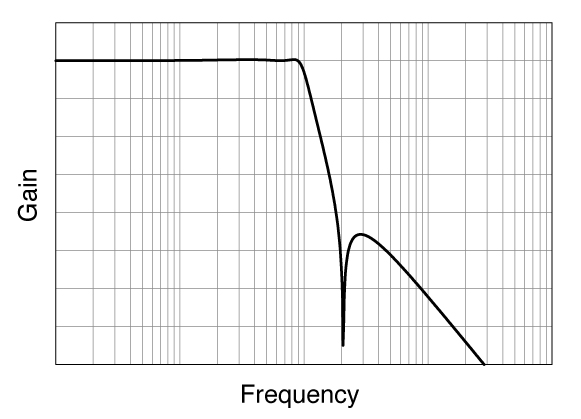
- 通過域、減衰域ともに、リプル (うねり) を持たせることで、遷移域を最小に出来るように考えられた特性
- 構成が大きくなると共に設計も高度になる
- 過渡応答でリンギングが大きい
【用途】
- できるだけ理想に近いフィルタ特性にしたい場合
- オーバサンプリングでないADコンバータのアンチエイリアス
各フィルタ特性における過渡応答
ここでは、各フィルタ特性における過渡応答 (ステップレスポンス) を比較してみましょう。
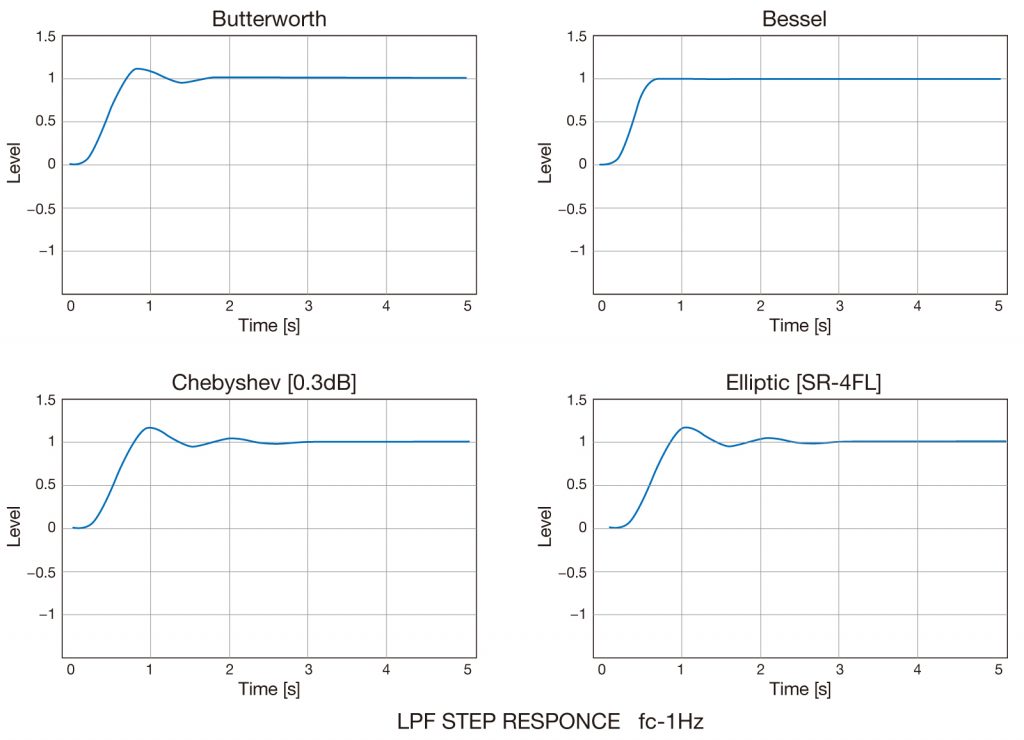
全体的に、「減衰傾度が大きいほど、リンギングが大きくなる」傾向にあります。
これは、各周波数での「位相のずれ=遅延時間の違い」によるもので、位相が周波数に対し直線であれば、入力される信号の各周波数成分の位相が、相対的にそろってフィルタから出力されるので、波形の変化は最小限で済みます。
しかし、ベッセル特性以外では、周波数に対する位相の変化は直線的ではなく、位相がずれて出てきます。これにより、オーバシュート、リンギングが発生することになります。
位相が直線のフィルタ
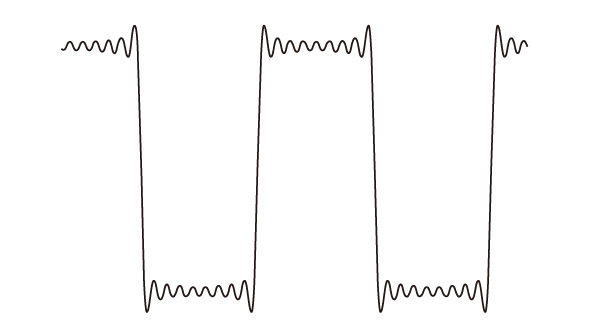
全てのスペクトルに対して位相は直線
位相が直線でないフィルタ
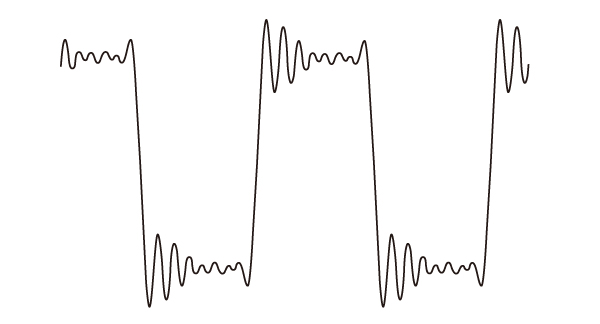
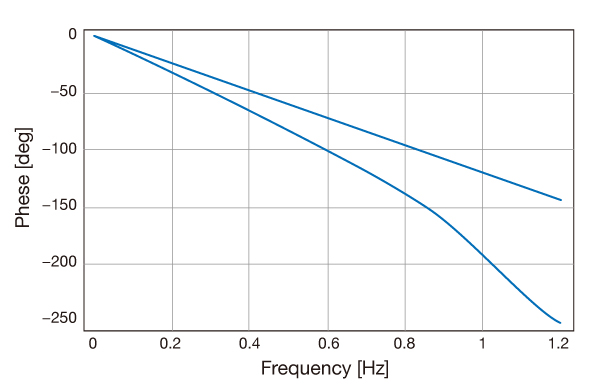
グラフ上の線がベッセル特性で、ほぼ直線で推移していることがわかります。
一方、グラフ下のチェビシェフ特性は、0.8Hz程度から曲がりはじめています。
このような非直線の位相特性が、立ち上がり特性を悪化させる原因となっています。
エヌエフのフィルタ
エヌエフでは、ベンチタイプとモジュールタイプのさまざまな用途に対応するフィルタを取り揃えています。
ベンチタイプのフィルタは、遮断周波数を自由に設定できる高機能フィルタをはじめ、特定の用途向けの製品もございます。
例えば、デュアルチャネルプログラマブルフィルタ 3628は、遮断周波数を1Hz~1.59MHzまで変化させて、最適周波数を決定する時に大変便利なフィルタです。
モジュールタイプフィルタは、次数、減衰傾度、減衰特性、周波数設定範囲などが決まっていれば、豊富な種類の中から最適なフィルタをお選びいただけます。面倒な設定なしに使用できますので、実験用や機器l組み込み用等、さまざまな用途で手軽にお使いいただけます。
4次系フィルタの製作
それでは、エヌエフのフィルタモジュールを使って、複雑な回路を簡単に製作してみましょう。
ここでは、通常設計が大変な上、調整にも時間がかかる4次系フィルタを例として取り上げます。
抵抗同調フィルタ SR-4BL2を使って、遮断周波数1kHzのローパスフィルタを製作します。
抵抗は、E96シリーズを使用します。
1. まず、抵抗値を求めます。
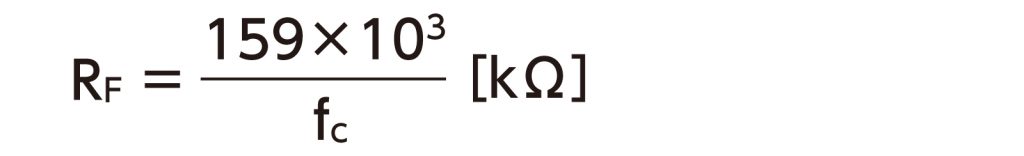
――――― (1)
ただし、Rf:抵抗値、fc:遮断周波数
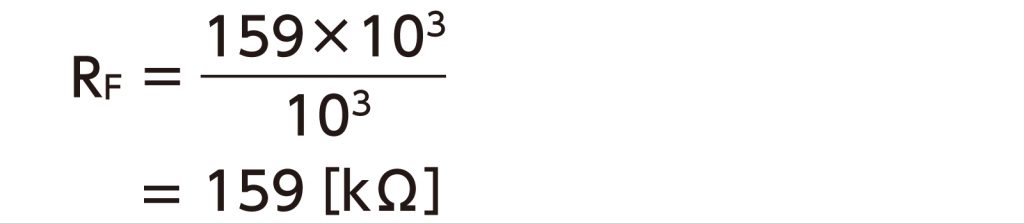
抵抗E96シリーズ(精度±1%)の公称抵抗値は以下の表の通りです。
| 100 | 127 | 162 | 205 | 261 | 332 | 422 | 536 | 681 | 866 |
| 102 | 130 | 165 | 210 | 267 | 340 | 432 | 549 | 698 | 887 |
| 105 | 133 | 169 | 215 | 274 | 348 | 442 | 562 | 715 | 909 |
| 107 | 137 | 174 | 221 | 280 | 357 | 453 | 576 | 732 | 931 |
| 110 | 140 | 178 | 226 | 287 | 365 | 464 | 590 | 750 | 953 |
| 113 | 143 | 182 | 232 | 294 | 374 | 475 | 604 | 768 | 976 |
| 115 | 147 | 187 | 237 | 301 | 383 | 487 | 619 | 787 | |
| 118 | 150 | 191 | 243 | 309 | 392 | 499 | 634 | 806 | |
| 121 | 154 | 196 | 249 | 316 | 402 | 511 | 649 | 825 | |
| 124 | 158 | 200 | 255 | 324 | 412 | 523 | 665 | 845 |
159kΩに一番近い値は、158kΩとなります。したがって、設定された遮断周波数は(1)式から、
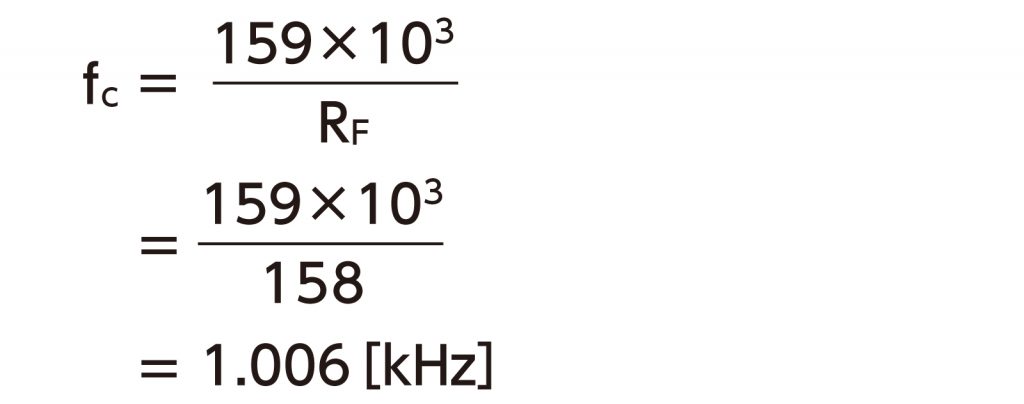
となります。
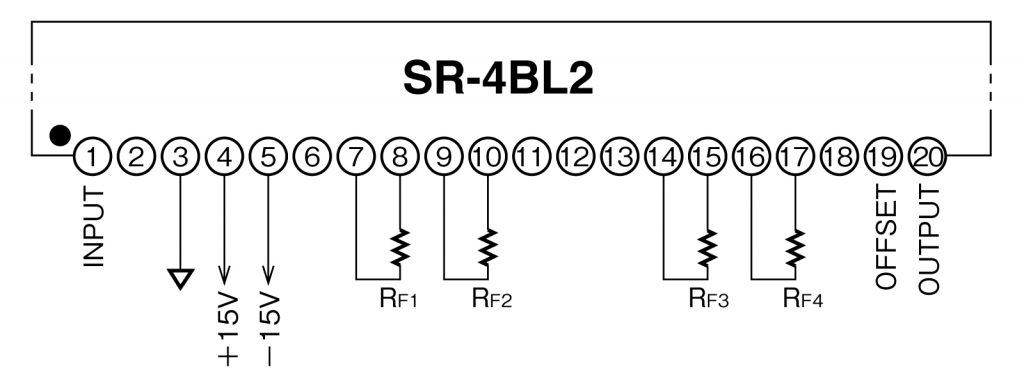
2. それでは、1で求めた抵抗を取り付けてみましょう。
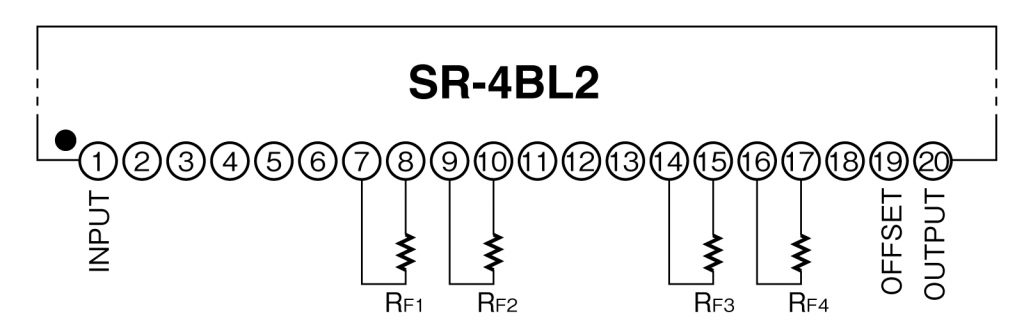
3. 次に電源の線を接続します。
4. バイパスコンデンサを取り付けます。フィルタのピンのすぐそばに取りつけてください。
セラミックコンデンサをご使用ください。
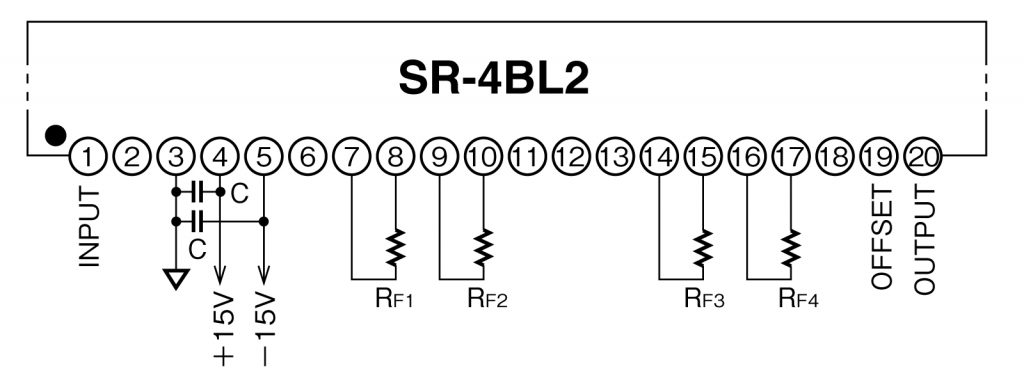
C:0.1μF
これで完成です。入出力を接続して電源を入れれば、動作します。
4次系フィルタの拡張と調整
遮断周波数を低域に拡張するには?
CFを外付けすることで、1Hzや0.1Hzといった低い遮断周波数の設定が可能となります。
この時、コンデンサは ±1%精度のコンデンサ (例えばフィルムコンデンサ)を使用してください。
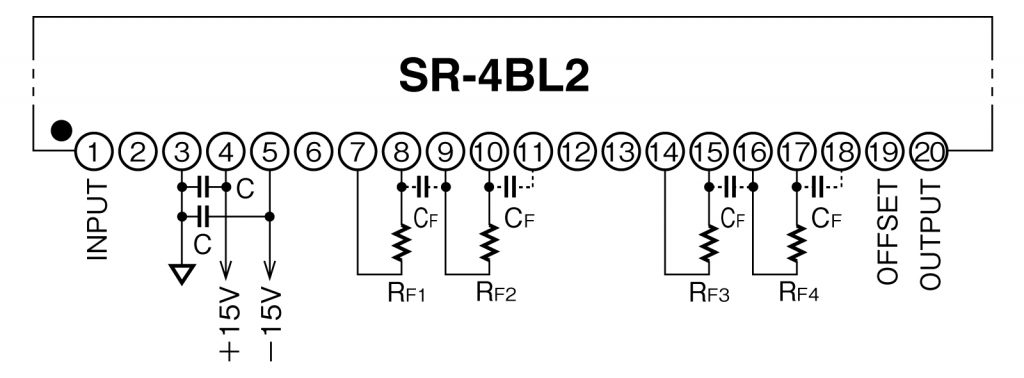
C:0.1μF
計算式は、以下のようになります。

オフセット電圧の調整
出力のオフセット電圧が気になるときは、調整ができます。ボリュームを接続してください。